benford.C

Benford's law on lifetime

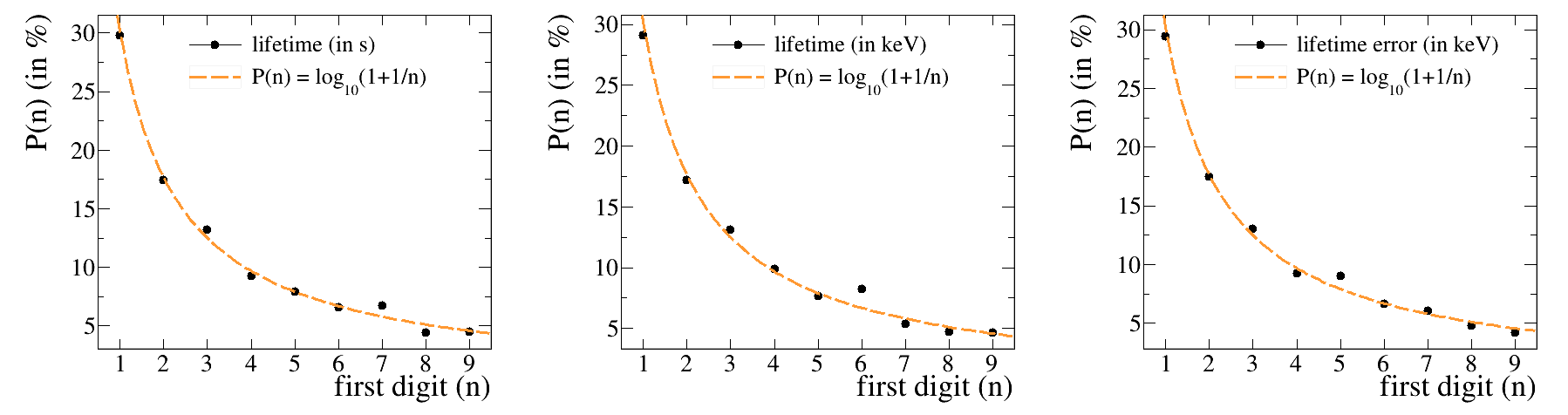
This example macro tests the benford's law on known excited state lifetime and uncertainty.

The Bendord's law (or first-digit law) states that in many real-life sets of numerical data, the leading digit is likely to be small. More precisely, the probability that the first digit is equal to n (n=1-9) writes (in base 10) : P(n) = Log₁₀(1+1/n).

This law applies approximately to any set of data covering many order of magnitudes and whose accessible values are not strongly constrained. Under these conditions, any strong deviation to the Benford's law can sign a bias in the measurement or a fraud.

Nuclear excited states lifetime are a perfect dataset to test the Benford's law. In this example, we build the first-digit probability distribution P(n) on lifetime values (expressed in second and in keV) and lifetime uncertainties (in keV) and compare them to the Benford's law prediction.

Start tkn-root, compile and execute this macro :

tkn-root
 _____    _   _   |  Documentation: https://tkn.in2p3.fr/
(_   _)  | \ | |  |  Source: https://gitlab.in2p3.fr/tkn/tkn-lib
  | |_  _|  \| |  |
  | | |/ /     |  |  Version 1.0
  | |   <| |\  |  |
  |_|_|\_\_| \_|  |  Database: TkN_ensdf_221101_xundl_210701_v1.0.db
 
tkn [0] .L benford.C+
tkn [1] benford()

It produces the following plots :

Source code :

#include "tkmanager.h"
#include "tkn_root_macros.h"
#include "tkstring.h"
#include "tkunit.h"
 
#include "TROOT.h"
#include "TCanvas.h"
#include "TH1.h"
#include "TF1.h"
 
using namespace tkn;
 
int first_digit(double value);
TH1* benford_level(std::function<double(shared_ptr<tklevel>)>const& eval, tkstring name="");
 
void benford()
{
    gROOT->SetStyle("tkn-histo");
 
    TF1 benford_law("Benford law","100*TMath::Log10(1+1/x)",0.5,9.5);
    benford_law.SetTitle("P(n) = log_{10}(1+1/n)      ");
    benford_law.SetMarkerStyle(0);
    benford_law.SetMarkerColor(benford_law.GetLineColor());
    benford_law.SetLineStyle(9);
 
    auto *cc = new TCanvas("benford","Benford's law on lifetimes",1800,500);
    cc->Divide(3,1);
 
    auto histo = benford_level([](auto lvl) {return lvl->get_lifetime(tkunit_manager::units_keys::s);},
    "lifetime (in s)");
 
    cc->cd(1);
    histo->Draw("");
    benford_law.DrawCopy("same");
    cc->cd(1)->BuildLegend(0.332776,0.779412,0.934783,0.936975);
 
    histo = benford_level([](auto lvl) {return lvl->get_lifetime(tkunit_manager::units_keys::keV);},
    "lifetime (in keV)");
 
    cc->cd(2);
    histo->Draw("");
    benford_law.DrawCopy("same");
    cc->cd(2)->BuildLegend(0.332776,0.779412,0.934783,0.936975);
 
    histo = benford_level([](auto lvl) {if(!lvl->get_lifetime_measure()) return 0.; return lvl->get_lifetime_measure()->get_error(tkunit_manager::units_keys::keV);},
    "lifetime error (in keV)");
 
    cc->cd(3);
    histo->Draw("");
    benford_law.DrawCopy("same");
    cc->cd(3)->BuildLegend(0.332776,0.779412,0.934783,0.936975);
   
   cc->cd(1);
    tkn::DrawLogoAndCredit(1.,5.,2,0.028,"Generated with");
   
    cc->SaveAs("benford.png");
}
 
TH1* benford_level(std::function<double(shared_ptr<tklevel>)>const& eval, tkstring name)
{
    glog.set_warnings(false);
 
    auto histo = new TH1F("digit",name.data(),9,.5,9.5);
    histo->SetName(name.remove_all(" ").data());
    histo->GetXaxis()->SetTitle("first digit (n)");
    histo->GetXaxis()->SetNdivisions(10);
    histo->GetYaxis()->SetTitle("P(n) (in %)");
 
    for(const auto &nuc : gmanager->get_nuclei()) {
        auto levelscheme = nuc->get_level_scheme();
        for(const auto &lvl : nuc->get_level_scheme()->get_levels()) {
            int fd = first_digit(eval(lvl));
            if(fd>0) histo->Fill(fd);
        }
    }
    histo->Sumw2();
    histo->Scale(100./histo->Integral());
 
    return histo;
}
 
int first_digit(double value)
{
    if(value<=0.) return 0;
    tkstring tmp = tkstring::form("%e",value);
    return tmp.substr(0,1).atoi();
}